概率论复习1

• 概率分布函数：概率分布函数是指定区间内随机事件（变量）发生（取值）的统计值分布规律的数学表示。即对于任意实数X，事件x在x<X范围内，每个点发生的概率分布函数可以表示为：F(x)=P(x<X)，显然0<=F(x)<=1，在给定区间a<=x<=b上，概率分布函数决定了事件(取值)x的发生概率，它反映了随机事件（取值）的统计特性。

• 概率密度函数：概率密度函数是随机事件（变量）在单位区间内发生概率的数学表示。

• 概率密度函数是概率分布函数的一阶导数

六种分布

1、0-1分布（伯努利分布）$B(1, p)$

• 概率分布函数：$P(X=x)=p^{x}(1-p)^{1-x}, x=0.1$
• 期望：$E(x)=P$
• 方差：$D(x)=P(1-p)$

2、二项分布$B(n, p)$

• n次独立重复的伯努利分布

• 概率分布函数：$P(x=x)=C_{n}^{x} p^{x}(1-p)^{n-x}$

• 期望：$E(x)=n p$

• 方差：$D(x)=n p(1-p)$

3、泊松分布$P(\lambda)$

• 概率分布函数：$P(x=x)=\frac{\lambda^{x}}{x !} e^{-\lambda}, x=0,1,2, \cdots$
• 期望：$E(x)=\lambda$
• 方差：$D(x)=\lambda$

4、均匀分布$R(a,b)$

• 概率分布函数：$f(x)=\left\{\begin{array}{cc}\frac{1}{b-a} & a \leqslant x \leqslant b \\0 & \text { 其他 }\end{array}\right.$

• 期望：$E(x)=\frac{1}{2}(a+b)$

• 方差：$D(x)=\frac{1}{12}(b-a)^{2}$

5、指数分布$E(\lambda)$

• 概率分布函数：$f(x)=\left\{\begin{array}{cc}\lambda e^{-\lambda x} & x>0 \\0 & x<0\end{array}\right.$
• 期望：$E(x)=\frac{1}{\lambda}$
• 方差：$D(x)=\frac{1}{\lambda^{2}}$

6、正态分布$N(\mu, \sigma^{2})$

• 概率分布函数：

$$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)$$

• 标准正态分布

$$f(x)=\frac{1}{\sqrt{2 \pi}} e^{\left(-\frac{x^{2}}{2}\right)}$$

• 期望：$\mu$
• 方差：$\sigma^{2}$

期望、方差、协方差、相关系数与矩估计

期望：

• $${E(X)=\sum_{k=1}^{\infty} x_{k} p_{k}}$$
• $${E(X)=\int_{-\infty}^{\infty} x f(x) \mathrm{d} x}$$

• 期望的性质

  • 设Y是随机变量X的函数$Y=g(X)$ g是连续函数

    • 如果$X$是离散型随机变量，它的分布规律是${P\left\{X=x_{k}\right\}=p_{k}, k=1,2, \cdots,}$若${\sum_{k=1}^{\infty} g\left(x_{k}\right) p_{k}}$绝对收敛，则有
    • $${E(Y)=E[g(X)]=\sum_{k=1}^{\infty} g\left(x_{k}\right) p_{k} }$$
    • 如果$X$是连续型随机变量，它的概率密度为$f(x)$，若${\int_{-\infty}^{\infty} g(x) f(x) \mathrm{d} x}$绝对收敛，则有
    • $${E(Y)=E[g(X)]=\int_{-\infty}^{\infty} g(x) f(x) \mathrm{d} x}$$

方差：

• $$\sigma^{2}=\frac{\sum(X-\mu)^{2}}{N} \\ {\sigma^{2}} 为总体方差， {X}为变量， {\mu}为总体均值， {N} 为总体例数。$$

• 方差还可以用公式：${D(X)=E\left(X^{2}\right)-[E(X)]^{2}}$

• 方差的定义式：$D(X) = E\{[X - E(x)]^{2}\}$

• 性质：

​

协方差：

• 协方差用于衡量两个变量的总体误差。方差是协方差的一种特殊情况，即当两个变量是相同的情况

• 期望值分别为 $E[ X]$与$E [ Y ]$的两个实随机变量$X$与$Y$之间的协方差 $Cov(X,Y)$ 定义为：

• $$\begin{aligned} \operatorname{Cov}(X, Y) &=E[(X-E[X])(Y-E[Y])] \\ &=E[X Y]-2 E[Y] E[X]+E[X] E[Y] \\ &=E[X Y]-E[X] E[Y] \end{aligned}$$

• 协方差与方差之间有如下关系：

  • $$D(X+Y)=D(X)+D(Y)+2Cov(X，Y)$$
  • $$D(X-Y)=D(X)+D(Y)-2Cov(X，Y)$$

• 协方差与期望值有如下关系：

  • $$Cov(X，Y)=E(XY)-E(X)E(Y)$$

• 协方差的性质：

  • $$Cov(X，Y)=Cov(Y，X)$$
  • $$Cov(aX, bY)=abCov(X，Y),（a,b是常数）$$
  • $$Cov(X_{1}+X_{2},Y)=Cov(X_{1},Y)+Cov(X_{2},Y)$$
  • $${\operatorname{Cov}(X+a, Y+b)=\operatorname{Cov}(X, Y)}$$

Pearson相关系数

• $${\rho_{X Y}=\frac{\operatorname{Cov}(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}}$$

• 若$\rho_{x,y}=0$，则称X与Y不线性相关

• 性质：

  • $$\left|\rho_{X Y}\right| \leq 1 \text {; }$$
  • $$|\rho X Y|=1 充分必要条件为 P\{Y=a X+b\}=1 ，(a ， b 为常数， a \neq 0)$$

---

卡方分布、F分布、T分布

卡方分布$\chi^{2}(v)$：

• 若n个相互独立的随机变量$\xi_{1}, \xi_{2}, ……, \xi_{n}$均服从标准正态分布$N(0,1)$，则这n个服从标准正态分布的随机变量的平方和 $Q=\sum_{i=1}^{n} \xi_{i}^{2}$ 构成一新的随机变量，其分布规律称为$\chi^{2}$分布，其中参数 $n=v$，称为自由度
• 正如正态分布中均数或方差不同就是另一个正态分布一样，自由度不同就是另一个$\chi^{2}$分布
• 当自由度$v$很大时，$\chi^{2}$分布近似为正态分布

​

• 性质：

​

F分布$F \sim F\left(n_{1}, n_{2}\right)$

• F分布是两个卡方分布除以其自由度之后的比值

• 若总体 $X \sim N(0,1),\left(X_{1}, X_{2}, \ldots, X_{n_{1}}\right) \text { 与 }\left(Y_{1}, Y_{2}, \ldots, Y_{n_{2}}\right)$ 为来自X的两个独立样本，设统计量

• $${F=\frac{\sum_{i=1}^{n_{1}} X_{i}^{2}}{n_{1}} / \frac{\sum_{i=1}^{n_{2}} Y_{i}^{2}}{n_{2}}}$$

• 则称统计量F服从自由度$n_{1}$和$n_{2}$的F分布，记为$F \sim F\left(n_{1}, n_{2}\right)$

• $$\frac{\chi^{2}(m) / m}{\chi^{2}(n) / n} \sim F(m, n)$$

• ​

T分布$t(n)$

• 假设$X$服从标准正态分布$N(0,1)$，$Y$服从$\chi^{2}(n)$分布，那么 $Z=\frac{X}{\sqrt{Y / n}}$ 的分布称为自由度为$n$的$t$分布，记为$Z \sim t(n)$

• $$\frac{N(0,1)}{\sqrt{\frac{\chi^{2}(n)}{n}}}\sim t(n)$$

• ​

• 随着自由度逐渐增大，t分布逐渐接近标准正态分布

大数定律与中心极限定律

切比雪夫大数定律

伯努利大数定律

​

辛钦大数定律

​

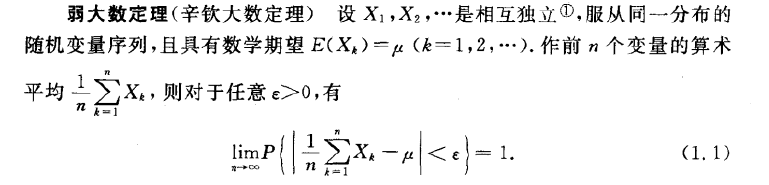
伯努利大数定律

​

中心极限定律

• 独立同分布的随机变量，构造一组新的变量，使之服从$N(0,1)$

• 定理一：

​

• 定理二：（定理一的特殊情况）

​