Attention原理介绍

概述

卷积、全连接、池化层都只考虑不随意的线索
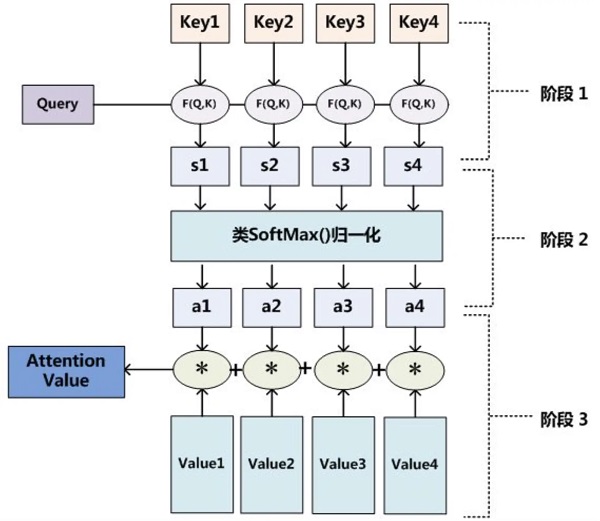
注意力机制则显式的考虑随意线索
- 随意线索被称之为查询query
- 每一个输入是一个值value和不随意线索key的对
- 通过注意力池化层来有偏向地选择某些输入，根据query有偏向的选择一些key-value pair
- 并不是所有的输入信息都是有用的，应当关心和qurey相似度最大的数据

给定数据$(x_{i}, y_{i}, i=1,\dots, n)$
平均池化使用最简单的方案$f(x)=\frac{1}{n} \sum_{i} y_{i}$
Nadaraya-Watsor核回归$f(x)= \sum_{i=1}^{n}\frac{K(x-x_{i})}{\sum_{j=1}^{n}K(x-x_{j})}y_{i}$，其中$f(x)$为query，$x_{j}$为key，$y_{i}$为value
- 使用高斯核$K(u)=\frac{1}{\sqrt{2\pi}exp(-\frac{u_{2}}{2})}$
- 则$f(x)=\sum_{i=1}^{n}softmax(-\frac{1}{2}(x-x_{i})^{2})y_{i}$

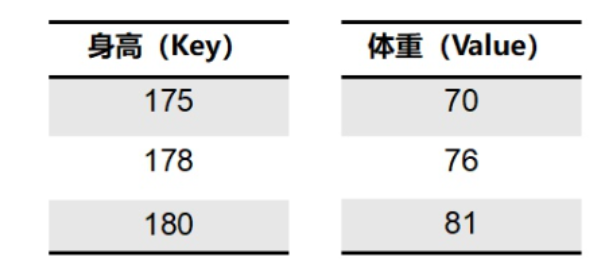
如果需要预测身高179的人的体重，由于179接近178与180，因此我们会非常注意178-76与180-81这两组key-value，
假设使用$\alpha(q, k_{i})$对应注意力权重，则Weight(q)可以表示为
$Weight(q)=\alpha(q, k_{1})v_{1}+\alpha(q, k_{2})v_{2}+\alpha(q, k_{3})v_{3}=\sum_{i=1}^{3}\alpha(q, k_{i})v_{i}$
其中$\alpha$是表示query与key之间相关性的函数，需要使用softmax归一化，使用高斯核为例：
$\alpha(q, k_{i})=softmax(-\frac{1}{2}(q-k_{i})^{2})$
高斯核函数用来计算数据之间的相似程度，得到的结果成为注意力分数，经过$softmax$归一化得到注意力权重
$\alpha(q,k_{i})=softmax(a(q, k_{i}))$
Attention机制的一般形式：$f(q)=\sum_{i=1}^{k}\alpha(q, k_{i})v_{i}$

模型名称	计算方法
加性模型	$\alpha\left(q, k_{i}\right)=v^{T} \tanh \left(W_{k} k_{i}+W_{q} q\right)$
点积模型	$\alpha\left(q, k_{i}\right)=q k_{i}^{T}$
缩放点积模型	$\alpha\left(q, k_{i}\right)=q k_{i}^{T} / \sqrt{d}$

以点积模型为例，$f(\boldsymbol{Q})=sofmax(\boldsymbol{Q}\boldsymbol{K^{T}} / \sqrt{d_{k}})\boldsymbol{V}$，其中$d_{k}$为特征维度，缓解梯度消失的问题（缩放点积注意力模型）

如果Q,K,V是同一个矩阵，此时计算为自注意力模型
$f(X)=softmax(XW_{Q}X^{T}W_{K}/\sqrt{d})XW_{V}$，$W_{Q}$，$W_{K}$与$W_{V}$分别是三个可学习的参数矩阵